Why I am not an Everettian

The many worlds interpretation seems to come up on top as the favored quantum interpretation among my friends. I have to admit, I chose the title mainly based on shock value, particularly aiming at said friends, and I do run the risk of being a bit misleading. So let me be very clear about my stance on the interpretation of quantum theory from the outset. ¹ Not only am I not an Everettian, I am also not a Copenhagenist, nor a Bohmian, nor a collapse-theorist. Of course, one might also infer from the fact that I am starting a quantum foundations blog that I am not Team SUAC (Shut Up And Calculate). My favorite quantum interpretation is None Of The Above, meaning that I don’t think we have figured out the correct way to interpret quantum theory yet. In fact, if you asked me to rank the existing interpretations, the many worlds interpretation probably would not be the one that comes out bottom. I think there are many aspects of the Everett interpretation that are very appealing. Nevertheless, I am not an Everettian, in the sense that I don’t believe many worlds is The Answer—and I hope you will think there are reasons to believe the same after reading this blog post.

In this post, I will first introduce the many worlds (Everett) interpretation, motivated as a solution to the measurement problem. Then, I will discuss several main issues with the Everett interpretation, and standard responses to them. In the end, I will sum up my thoughts on why I am ultimately not an Everettian.

The measurement problem, relative states, and many worlds

The measurement problem might be the most commonly cited issue with standard quantum theory. This problem refers to the conflict of two postulates in the standard quantum recipe: ²

• Evolution of isolated systems is unitary, which is deterministic and continuous.
• When a system undergoes a measurement, an outcome occurs in random according to the Born rule, and the quantum state of the system is updated to the eigenstate corresponding to the measurement outcome.

When applied to the system and measurement apparatus as a whole, it is clear that the two axioms are in conflict: one predicts deterministic and continuous evolution, while the other one predicts nondeterministic and discontinuous evolution. This is the most straightforward version of the measurement problem.

In the 1950s, while still a graduate student, Hugh Everett III realized that one way to solve this problem is to simply reject one of the above postulates. In particular, he decided to reject the second, which is often called the collapse postulate. So everything everywhere always undergoes unitary evolution, including systems undergoing measurements. Insteading of collapsing from time to time, the wavefunction of the measured system simply becomes entangled with that of the measurement apparatus, and everything in the universe gradually becomes part of one gigantic, crazily-entangled wavefunction.

How can such an egregious object make any sense? And what about the fact that observers seem to have definitive experiences? After all, the starting point of many other interpretations is that such a wavefunction cannot describe the reality after measurement, in which a definite outcome had occured. It is useful here to introduce some concrete mathematics. (As an aside—My goal in this blog is to not assume any background beyond one semester of college-level quantum mechanics.) Say we are carrying out a Stern-Gerlach experiment to measure the spin of a particle in the $z$ direction. The quantum states corresponding to the two outcomes of the spin are labeled $\ket{\uparrow}$ and $\ket{\downarrow}$, and the quantum states describing the measurement apparatus after the measurement are $\ket{\text{observed} \uparrow}$ and $\ket{\text{observed} \downarrow}$. If the incoming particle is in state $a\ket{\uparrow} + b\ket{\downarrow}$, then the particle together with the apparatus after the measurement is in state $$ a \ket{\uparrow} \ket{\text{observed} \uparrow} + b \ket{\downarrow} \ket{\text{observed} \downarrow}.$$ Is there a way to understand this quantum state as describing the world after a measurement has occured with a definitive outcome?

Everett came up with one, and termed his solution to this problem the “relative state”. In fact, his PhD thesis in which the bases of this interpretation were laid was called “[The] ‘Relative State’ Formulation of Quantum Mechanics”, and the thought-provoking term of the “many worlds interpretation” was only coined by Bryce de Witt and Neil Graham some fifteen years later. The idea of the relative state is essentially that, the measurement device did register a definitive outcome (“observed up” or “observed down”), relative to the spin of the particle being up or down. It is clear that if another measurement is carried out, say, if we immediately put the particle through a Stern-Gerlach device in the $x$-direction, the same mechanism applies and we just get a wavefunction that is more entangled. This way, each time a measurement occurs, the wavefunction simply branches in configuration space, but everything in the universe is still described by one wavefunction, albeit enormous and more and more complicated. This is called the universal wavefunction. The Everettian simply takes the picture regarded as wrong and problematic before as literally true. The consequence of this leap of faith is profound: this means that the universal wavefunction branches further and further each time something that constitutes a measurement occurs, and all of the possible combinations of outcomes play out in parallel in many parallel worlds.

This is no doubt an elegant and revolutionary solution to the measurement problem, and it comes with profound implications. Indeed, many proponents of the many worlds interpretation seem to be drawn to the theory by this sense of elegance and boldness, which I personally find somewhat compelling as well. I’m all for taking seriously the logical implications of good ideas, even if that means accepting a dizzying multitude of worlds. But how well does this work as a solution to the measurement problem? And does this picture give us a coherent theory that matches observed reality in the first place? These are the questions I will try to assess in the rest of this post. In the subsequent sections, I will explore three issues commonly raised about this interpretation, ordered roughly by the degree to which they are troubling to me.

The problem of preferred basis

The basic picture of the Everettian worldview is that the universal wavefunction branches with each measurement, into parallel worlds, each of which is as real as the one you and I are experiencing at this moment. This immediately begs the question: What determines the branching structure of the wavefunction? After all, choosing a branching structure is nothing more than choosing a basis. But if one accepts Everett’s theory, then this choice is physically significant, as it determines the set of possible real experiences.

More concretely, in the above example, the universal wavefunction of the particle and the measurement device is $$ a \ket{\uparrow} \ket{\text{observed} \uparrow} + b \ket{\downarrow} \ket{\text{observed}\downarrow} $$ after a Stern-Gerlach measurement. But this expression is mathematically equal to this rewritten version, $$ \left( \frac{a \ket{\uparrow} + b \ket{\downarrow}}{\sqrt{2}} \right) \left( \frac{\ket{\text{obs}\uparrow} + \ket{\text{obs}\downarrow}}{\sqrt{2}} \right) + \left( \frac{a \ket{\uparrow} - b \ket{\downarrow}}{\sqrt{2}} \right) \left( \frac{\ket{\text{obs}\uparrow} - \ket{\text{obs}\downarrow}}{\sqrt{2}} \right). $$ What in the theory singles out the first one as the correct branching structure, and not the second one? This is particularly troubling, because if the second expression were the one that dictates the branching structure, then the observer in each branch no longer has a definitive experience.

While Everett himself seems to be of the view that all possible branching structures are real—a position I don’t quite know how to make sense of—there have been a number of attempts at specifying a rule for the branching structure, including one that appeals to a preference for deterministic evolution over an indeterministic one. However, it is my understanding that the typical modern Everettian no longer agrees with either of the above approaches. It appears that the mainstream response among modern Everettians is largely one that this is not a problem for them to solve. Specifically, they claim that the theory does not have to specify a rule for determining the branching structure, because all “real” objects in the theory comes from processes of decoherence and emergence. Of course, the only ontologically ³ real thing is the universal wavefunction; familiar entities in our daily lives merely emerge from the universal wavefunction as patterns, and in particular, useful patterns. By “useful” here, I mean that they have explanatory and predictive power.

David Wallace, for example, famously employs the analogy of a tiger: there are no tigers in the Standard Model, but we nevertheless regard a tiger as “real”, not only because it is made up of particles that are part of the Standard Model, but also because the concept of a tiger is useful—it might impose serious danger to the safety of humans! Wallace argues that the way our perceived reality emerges from the universal wavefunction is similar. Other examples thrown around include the concepts of a mountain or a species: we think that mountains and species are “real”, because they are useful concepts for us to have in life, even though they do not feature in our fundamental laws of physics, nor can one really define the exact boundaries of a mountain or a species. Therefore, the Everettian theory does not need to specify a rule for the branching structure; instead, the branching structure selected by the theory is the one in which useful patterns emerge. Going back to the above example, the first basis is selected whereas the second is not, because it is useful to think about observers that “observe up” or “observe down”, and not as useful to think about observers that have experiences that correspond to a superposition of the two.

To me, this response is less than satisfactory. As I will elaborate in the concluding section, this and many other responses of the Everettian sound less like an explanation and more like a clever evasion of the question. But this sets me up nicely to discuss the next problem: the ontology problem.

The ontology problem

A hallmark of the Everett interpretation is the position that “the wavefunction is all there is”. However, this does not seem to be the direct experience of you and me. Indeed, we seem to live in a three-dimensional world, which is filled with three-dimensional objects. The wavefunction, on the other hand, lives in a completely different space, the configuration space. This space has much higher dimensions—its dimension scales exponentially with its number of constituents. In order for Everett to be an adequate interpretation of quantum theory, it has to explain how the physical world that we perceive arises from an object as exotic as the wavefunction.

The usual story here is again “emergence”, as I started discussing a bit above. The Everettian would say that the 3D world we perceive emerges out of the wavefunction in the same fashion that a tiger emerges out of its microscopic constituents. If one thinks for a little while though, this analogy does not quite make sense—at least not much to me. The problem is, no matter how microscopic the particles that make up the tiger are, they are still localized entities in three-dimensional space, and we are simply talking about a bigger object emerging out of smaller ones. However, the wavefunction is a totally different beast, and it is completely unclear how the process of emergence works in this case.

Fields, which underlie most of modern physics, are sometimes used as another example in this argument—aren’t they kind of weird too? Sure, they are a bit weirder than microscopic particles, but one should still be much more comfortable with the ontological status of fields, compared to that of the universal wavefunction. The claim that the laptop in front of me “emerges” out of Standard Model fields is a lot more benign, since fields are still objects living in 3D space, albeit no longer localized. Comparing the wavefunction to fields is understating the weirdness of the ontological status of the wavefunction. Since the wavefunction lives in a completely different kind of space, more explanation than simply “emergence” is needed.

There have also been attempts at positing additional ontological entities in many worlds theories, but my understanding is that those are not popular within the Everettian community. (Or, you get something that starts looking very much like the de Broglie-Bohm theory…) Generally, the response is still that emergence takes care of everything. Of course, another angle to approach this problem is to go one step further, and suggest that perhaps the three-dimensional world we perceive is a mere illusion. There is nothing fundamental about it, and so the many worlds interpretation does not have to explain how it arises. But if we were to go there, I think I will need some otherwise very good reasons to believe that the Everettian theory is a theory about our world at all. It seems to me that the two ways out of the ontology problem are 1) posit additional ontology, which is regarded as inelegant, or 2) take some leaps of faith about the emergence of the real world, which I’m hesitant to do.

The problem of probabilities

The third and perhaps most troubling problem with the many worlds interpretation is the problem of probabilities. How can we make sense of probabilities in an Everettian universe? How can anything be probabilistic at all in a theory that is completely deterministic? Furthermore, how in particular does the Born rule arise as the quantatitive measure to weigh the relative probabilities of the outcomes? After all, all that the quantum recipe specifies are the relative probabilities of events, described by the Born rule. In order for Everett to be a satisfactory interpretation of quantum theory, it needs to explain the role of the Born rule.

Consider, for example, a series of Stern-Gerlach experiments carried out on identically prepared particles, in the state $(\ket{\uparrow} + \ket{\downarrow})/\sqrt{2}$. For each individual measurement, quantum theory predicts that the outcome is “up” or “down” with equal probability. One can draw a tree documenting all possible sequences of outcomes obtained in these experiments, shown as below. The traditional understanding is that this is a tree of possibilities, and one finds oneself on any leaf of the tree with equal probability. According to Everett, however, this is a tree of actual, equally real worlds, all of which exist in parallel. One immediately sees that the meaning of probability has to be different in the Everett interpretation—every possible sequence of outcomes actually happens in a world, with certainty. The best way to make this problem acute is to consider the problem of theory confirmation: Why should we be very surprised if the outcomes are all “up” if we carried out $N$ Stern-Gerlach experiments in a row? After all, there is one world in which this sequence of events happened with certainty!

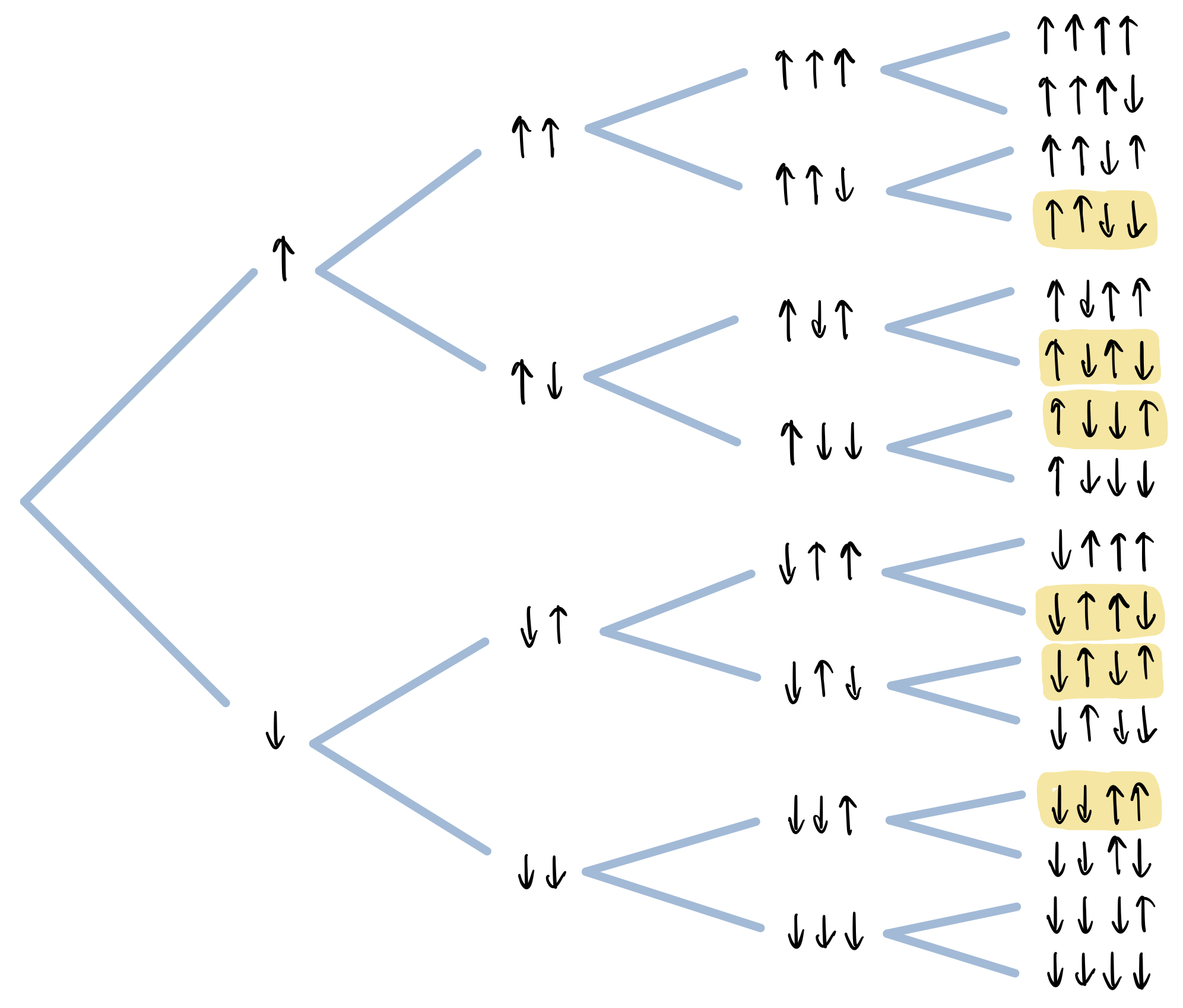
The canonical way to reproduce some notion of probability is by resorting to the relative frequency of worlds that appear in the branching structure. For example, in the above example, after performing the Stern-Gerlach experiment 4 times, we notice that in 6 out of the 16 worlds, the observer has seen outcome “up” twice and the outcome “down” twice. One can easily convince oneself that this is the most likely statistics after 4 measurements. It is not hard to generalize this to $n$ Stern-Gerlach experiments, after which there would be $2^n$ worlds, and in $n \choose n/2$ (read: $n$ choose $n/2$) of those worlds “up” and “down” will have an occurred equal number of times. It turns out that when $n$ is large, the function $f(x) = {n \choose x}$ is well-approximated by a Gaussian centered at $n/2$ with standard deviation $\sqrt{n}/2$. This means that the most likely statistics for an observer to have observed after $n$ Stern-Gerlach experiments is for $n/2$ of them to turn out “up” and $n/2$ of them to turn out “down”, which exactly matches the prediction of the Born rule.

It is pretty straightforward to see, however, that this construction really only works when the two outcomes occur with equal probability. If the particle is now prepared in a general state $a\ket{\uparrow} + b\ket{\downarrow}$, the branching structure is the same as before, and we can still draw the same tree. The same counting argument would tell us that the most likely statistics is still observing outcome “up” half of the time, instead of observing outcome “up” with probability $|a|^2$ as predicted by the Born rule. The solution to this is to use a different measure over the branches, i.e. assign them different weights. This seems at least in spirit in conflict with Everett’s original idea that “no world is more real than others”. Of course, the bigger problem is that we are now in somewhat of a circular logic: in order to reproduce Born rule statistics, we need to weigh the branches by the squared magnitude of their amplitudes, which was given by the Born rule in the first place.

There have been some more creative attempts at the problem of deriving the Born rule. David Deutsch was one of the first to approach this problem from a decision-theoretic point of view. This is inspired by the view that probabilities are only meaningful insofar as rational agents make choices based on them to maximize their utilities. Since then, there has been a line of work aiming to show that a rational Everettian must act as if the squared amplitudes of future branches were probabilities, in the sense that they would make the same decisions as a regular agent maximizing expected utility in the face of indeterminism. Essentially, the goal is to show that certain principles of rationality forces Everettian agents to adopt a “caring measure” over all the possible branches, and this measure is exactly the one that reproduces the Born rule. In his 2012 book, David Wallace shows that starting from a decision-theoretic framework and a few axioms motivated by rationality leads one to the above conclusion.

There are a few criticisms one can pursue with this result. First of all, it is unclear whether the axioms that serve as the starting point of Wallace’s theorem are well-motivated, or actually capture the notion of rationality. For example, some of the arguments invoke an “indifference principle”, asserting that the Everettian agent must regard certain decision problems as equivalent for all decision-theoretic purposes. This sort of indifference implies being indifferent to many physical facts, and it is not clear why the agent must be indifferent to exactly these physical facts but not others. As another example, this framework demands that no rational agent can directly desire to create certain sorts of branching structures and value the existence of such structures more highly than the existence of either branch individually. This strikes me as a bit philosophically awkward—in fact, Tim Maudlin points out that it is strange that Everettians do not seem to believe the heretofore unrecognized branching structure should have any surprising practical consequences for everyday life. To me, this suggests a certain sense of not taking the ontology of their own theory seriously.

By far the weightier criticism, however, is the question of whether or not results like this really serve the purpose of explaining the role of the Born rule in the quantum recipe. David Albert’s criticism comes to mind: it is not enough to show that an agent who believes in the Everettian picture must bet in accordance with the Born rule; one must explain why we observe the particular relative frequencies of outcomes that we do. The decision-theoretic approaches to the problem of probability all have a strong normative flavor—meaning that they are concerned with how agents ought to behave in certain situations—and it is simply the case that there are non-normative facts to be explained. ⁴

Concluding thoughts

Let us now take a moment and tally up the points. What are some points in favor of the many worlds interpretation? It definitely gets some points for proposing an elegant solution to the measurement problem. However, it is useful to keep in mind that there are many other ways to resolve the measurement problem, and solving the measurement problem is only one of the bars a satisfactory quantum interpretation has to pass. I think Everett also gets some points for being “minimalist”, or favored by Occam’s razor in some sense. The whole theory rests on one simple yet radical change to the quantum postulates. For example, there is definitely a sense in which many worlds is more parsimonious than Bohmian mechanics, which according to some is essentially the universal wavefunction plus additional ontology. However, this flavor of minimalism seems very “Schrödinger-equation-centric”. By that, I mean that the minimality only shows up if one frames quantum theory in terms of the standard postulates with the Schrödinger equation. Without a preconceived ontology, it is unclear why it makes sense to take the Schrödinger equation at face value; and if one opens oneself up to other equivalent formulations of quantum theory, then other interpretations would be favored as equally or even more minimalist, e.g. quantum logic.

The ultimate question one needs to evaluate is this: for all the points that Everett scores and the amount of explanatory power it offers, is it a good tradeoff with the philosophical cost that it demands one pay? Before I give my answer, let me first make clear why I think this is the right question to consider. The fact that there is no consensus on the interpretation of quantum theory to this day means that we are clearly missing a piece of the puzzle, and the eventual solution probably requires us to stretch our imagination and abandon some notions that were previously deemed fundamental. The candidate solutions on the table should all have this radical flavor. In this context, the interpretations will have to be judged by considering the tradeoff between the explanatory power it offers and its cost. Let me also be clear about what I mean by “philosophical cost”—I’m essentially echoing Matt Leifer’s blog post on many worlds here—this refers to the fact that certain changes to our knowledge system are more costly than others, similar to how a bowl that is chipped on the rim can still hold water fine, whereas a bowl that is chipped at the bottom is going to have a lot more trouble. We should consider it more costly and hence be more skeptical when a theory is proposing more fundamental changes to our current structure of scientific knowledge, because it is necessarily going to be harder to reconstruct all the dependent knowledge further up the bowl.

In the case of Everett, I am not convinced that the tradeoff is worth making. Everett is incurring a high philosophical cost by demanding many radical deviations from our scientific theories to date, and the gain in explanatory power is really in my view not enough. As we saw in the discussion of the above three problems, Everett still struggles with explaining many aspects of quantum theory and our observed reality. It seems to me that the starting point of Everett is taking a mathematical description of quantum theory to be literally true, and then trying to come up with clever arguments for why this might be a theory that describes our reality. While this is an illustrative exercise to go through—and I even think the community has arrived at OK arguments for some of the problems—ultimately, I think there is very little going for Everett beyond the starting point of a “minimalist solution to the measurement problem”. At the very least, we need to be pretty sure that there isn’t an equally good alternative theory that demands fewer radical changes before accepting it.

Finally, I do recognize that my unfavorable view of Everett comes partially from its conflict with a position that I favor more. I plan to devote one of the next blog posts to this topic—to me, the evidence that the quantum state is a state of knowledge is overwhelming. The many worlds interpretation, viewing the wavefunction as not only ontic (i.e. real) but also complete (i.e. all there is), seems to fundamentally miss the clues about what type of object that wavefunction is. As just one example, the exponential scaling of the number of branches is characteristic of a space of possibilities, rather than a space of actualities. To me, this is yet another piece of evidence for the epistemic nature of the wavefunction, and taking it as the only real entity in one’s theory seems fundamentally misguided. But this is a story for another time.