Is the quantum state a state of knowledge?
Jun 07, 2022
A category mistake
On the early morning of September 14, 1822, a young Frenchman named Jean-Francois Champollion was running through the streets of Paris. He burst into his brother’s office at the Académie des Inscriptions, and shouted, “Je tiens mon affaire!” (“I’ve done it!”), before collapsing on the floor. Champollion had just become the first person able to read ancient Egyptian hieroglyphs in two thousand years.
Following the sleepless nights that led to this historic achievement, Champollion would immediately succumb to a week-long, exhaustion-induced illness, and the decipherment of Egyptian hieroglyphs would go down in history as one of the best examples that demonstrate how simple, incorrect assumptions can drastically hinder scientific progress. In this particular case, the roadblock amounted to one simple assumption about the nature of the hieroglyphs, what type of objects they are—a category mistake. For generations, scholars studying the script believed that the hieroglyphs are ideographic, meaning that they are symbols that represent ideas. However, as Champollion had eventually figured out, this was a false premise. Much of the Egyptian hieroglyphic script is in fact phonetic, with symbols representing sounds.
How did the belief that the hieroglyphs were ideographic come into being in the first place? Efforts to decipher Egyptian hieroglyphs started not long after the Ancient Egyptian scripts ceased to be understood in the fourth century BC. Rather unfortunately, pretty much all scholars who worked on the decipherment had assumed that the hieroglyphs are ideographic from the get go, perhaps due to their extremely visually suggestive nature. The result of such an assumption was a stall in progress for essentially a millennium. No matter how hard people tried, they could not figure out what ideas corresponded to which symbols. And this was not due to a lack of imagination. In his treatise on the subject, Hieroglyphica, Ancient Greek scholar Horapollo showcased his extraordinary imagination with his theory on the meaning of 189 hieroglyphs. For example, let’s take a look at these three symbols:
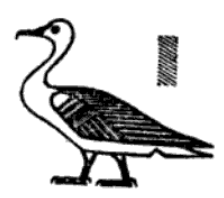


According to Horapollo, the first of these hieroglyphs means “son”, represented as a goose. This is because—reasons Horapollo—the goose is excessively fond of its offspring, and routinely sacrifice their own lives to preserve those of its young. The second bird is an ibis, and according to Horapollo means “heart”, both because it resembles the shape of a heart and that the ibis is “consecrated to Hermes [Thoth], the lord of every heart and of reasoning”. The third bird is a swallow, and represents “the whole of a parent’s substance has been left to the sons”. This is because “[a swallow] rolls herself in the mud, and builds a nest for her young, when she is herself about to die”.
Now, the first of these interpretations is actually known to be correct—Horapollo lived fairly close in time to people who knew the hieroglyphs, and it looks like some genuine knowledge about the script was retained. But it is not for the reasons that Horapollo thought. Instead, the goose symbol represents the syllable “sꜣ”, which is the pronunciation of the word for “son” in the spoken language of Ancient Egyptians. 1 Needless to say, most of his interpretation are now proven to be complete nonsense. Nevertheless, the harm was done. Even though some of these interpretations are so wildly speculative that they probably were never taken as true, scholars pursuing the decipherment of the hieroglyphs following Horapollo’s footsteps internalized the premise that the hieroglyphs are ideographic.
As a result, it was not until the discovery of the Rosetta Stone that real progress started being made. The Rosetta Stone, discovered by Napoleon’s army in 1799, bears the exact same passage of text in three different scripts: hieroglyphs on top, Ancient Greek at the bottom, and an unidentified script (later to be deemed Demotic, a different type of Ancient Egyptian script) in the middle. Since Ancient Greek was still a known language, this enabled a direct side-by-side comparison of the languages. It’s basically as close as we could hope to get to a dictionary.
Even then, the hieroglyphs were not deciphered right away. Soon after the discovery of the Stone, scholars such as Thomas Young had correctly figured out that the parts of the text that were enclosed in little ovals, named “cartouches”, correspond to names of Egyptian kings. Building upon the work of Young and others, our hero Champollion was able to deduce that the cartouches below spelled the names “Ptolemy” and “Cleopatra”, and he was able to identify the phonetic values of some hieroglyphs by comparing the two names.
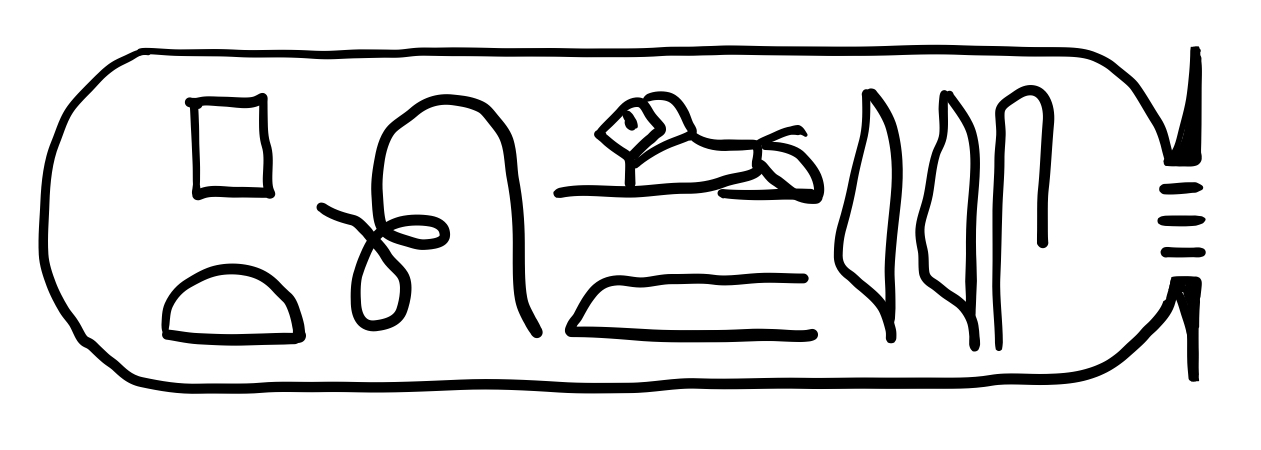
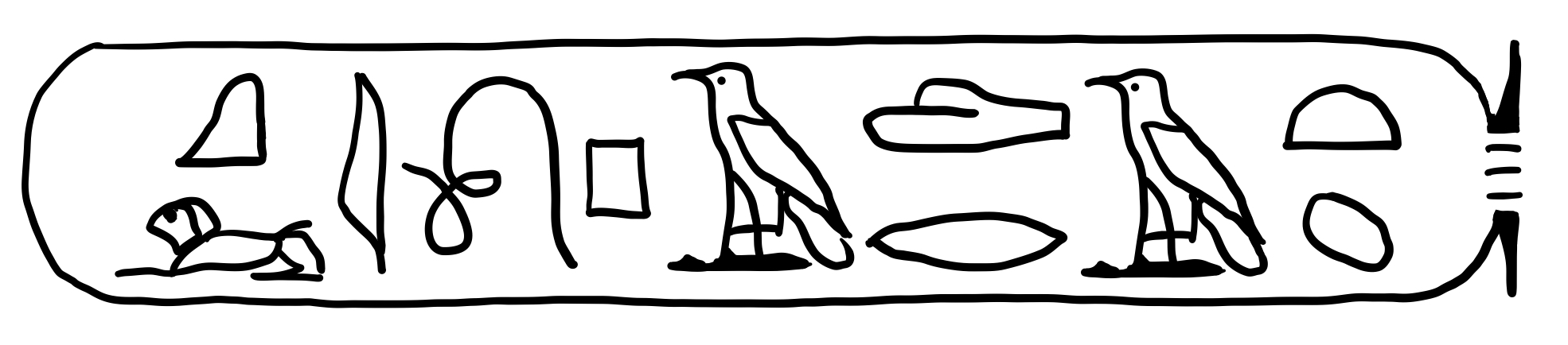
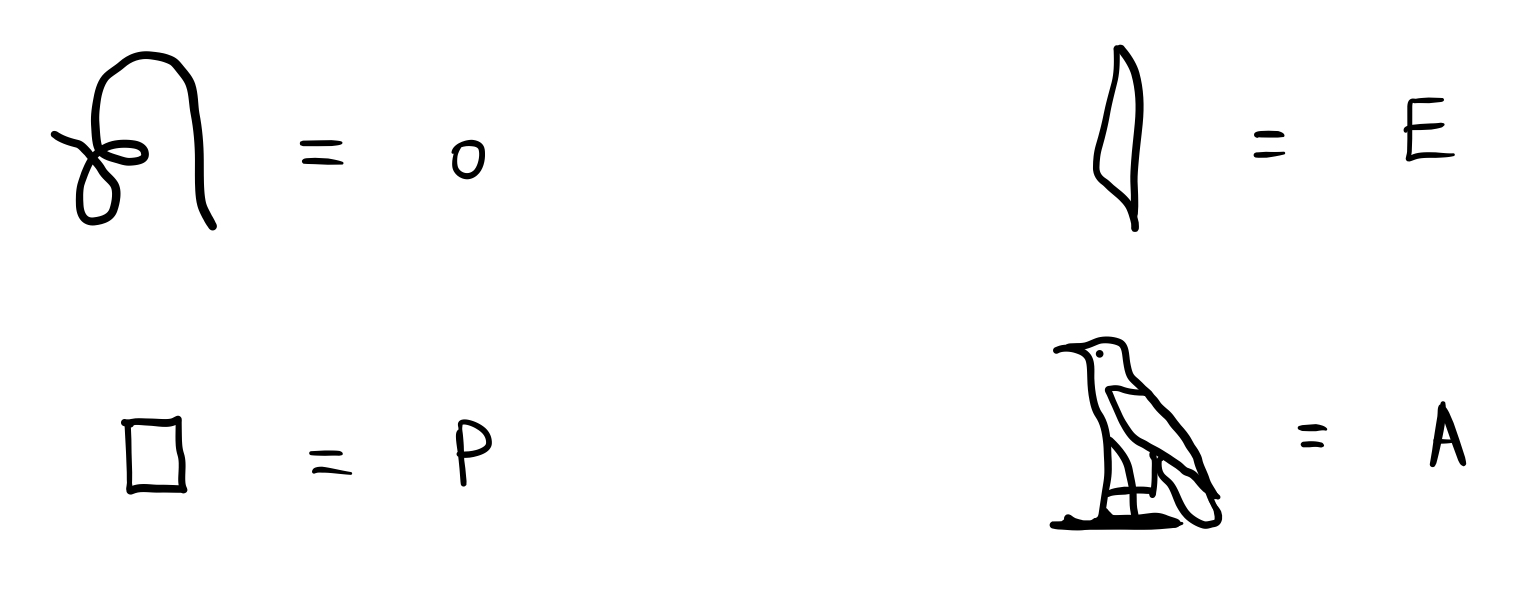
However, even then, Champollion did not go on and decipher the rest of the script right away. The idea that the hieroglyphs were ideographic was so entrenched in his mind that he thought only names of foreign origin were spelled out phonetically, as were Ptolemy and Cleopatra. It was not after many more months of effort without progress did Champollion finally start to entertain the idea that perhaps hieroglyphs can be phonetic outside of cartouches. As soon as he started looking at the text with this new assumption, he immediately started to recognize familiar phonetic elements from a language that was still in use and that he was familiar with, Coptic. 2 This was it. It turns out that the Egyptian hieroglyphs are essentially another alphabet for the spoken language of Coptic, and Champollion would land on the floor of his brother’s office a few days later. 3
$\psi$-onticity: another category mistake?
I love the story of the decipherment of the hieroglyphs, and what it teaches us about how bafflingly costly a category mistake can be. Of course, I’d better start talking about the foundations of quantum theory before you start wondering what happened to this blog and stop reading. The reason why I’m bringing up the tale of deciphering hieroglyphs—besides that I really love good stories—is because I want to ask the following question: Could the reason why we have been stuck on the interpretation of quantum theory be that we are making a similar category mistake? By assuming that the hieroglyphs are ideograms, scholars were stumped for a millennium, while the spoken language of Coptic was being passed on from generation to generation. What could be a possible incorrect assumption that we have been making in the interpretation of quantum theory?
Before I discuss the candidate assumption that I have in mind, I need to first define a very important distinction: ontic versus epistemic. Loosely speaking, something is ontic if it is real, or corresponds to an element of reality, and something is epistemic if it corresponds to the knowledge possessed by some agent. While this is by no means a clear distinction, and it can sometimes be tricky to judge whether something is ontic or epistemic, a simple puzzle comes in handy to illustrate this distinction:
You move to a new town to start a new job. On your new daily commute, you drive by this billboard every day, but unfortunately the display seems to be broken. How would you go about figuring out what the billboard is supposed to say?
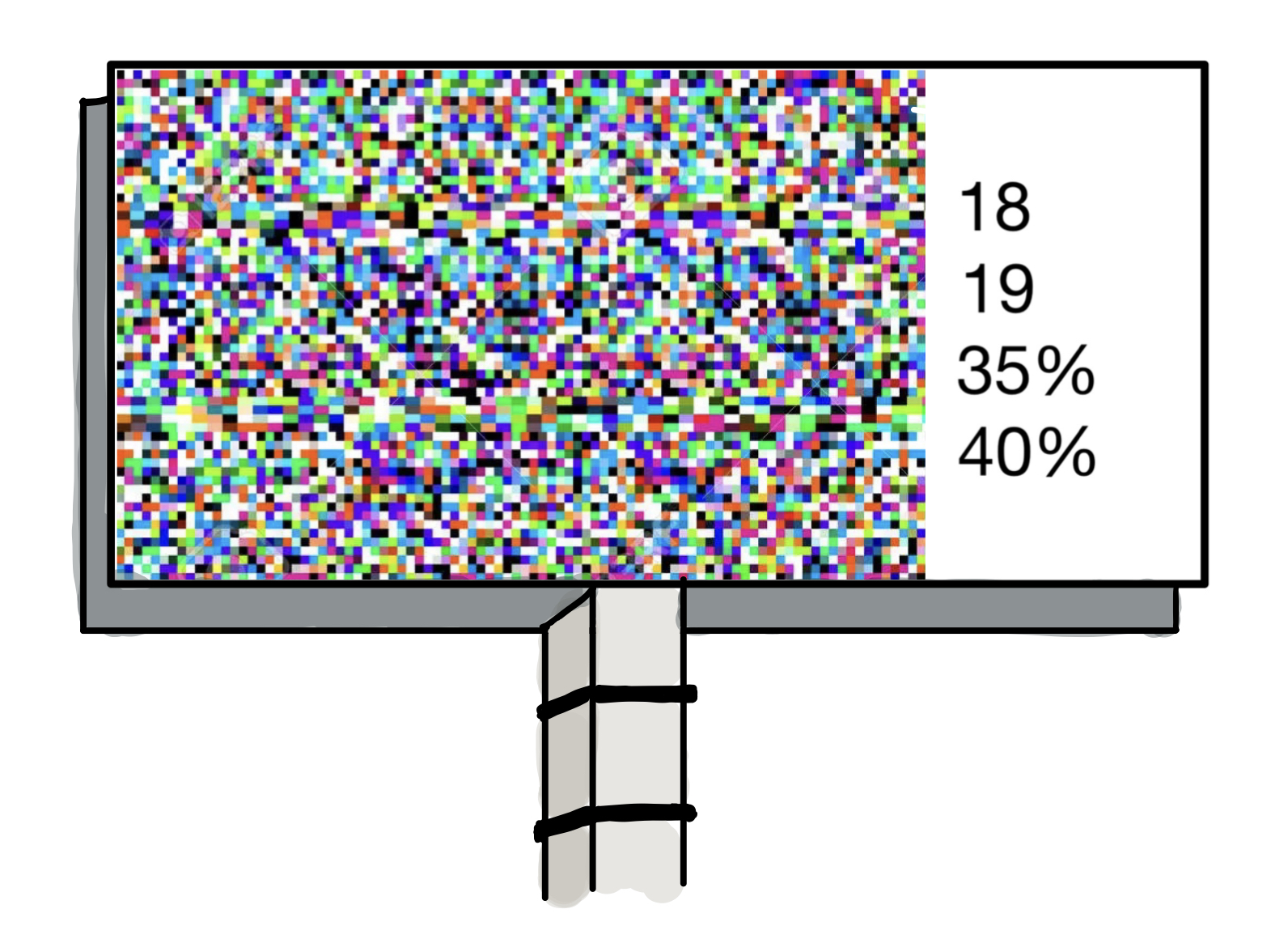
The numbers on the billboard change every day, so you suspect that the numbers have to do with weather. Enjoying a little challenge, you decide to conduct your own experiments to figure out the meaning of the numbers. You go and buy a thermometer (or use a clever contraption of your own devising, if you prefer), and see that the highest temperature of the whole day is 18 degrees Celsius when the first entry on the billboard says 18. Aha! Similarly, you measure the wind speed, and realize that the second entry says 19 when the wind speed, averaged over the whole day, is about 19 kilometers per hour. The third one takes you a bit longer to figure out. Eventually you decide to take a bunch of pictures of the local sky, and you find that the billboard says 35% when 35% of the sky is covered by clouds on average. 4 You are a bit stumped by the fourth one, though. You keep measuring more and more weather-related quantities, but you can’t seem to find anything that is 40% when the billboard says 40%.
Eventually, after many weeks of effort, (thankfully, everything takes forever to fix so you get to continue carrying out your investigation), you sit down to tally up all the data you have collected so far. You realize that out of all the days that the billboard said 40% for the last entry, it rained on about 40% of them! Similarly, out of all the days that the billboard said 80%, it rained about 80% of the time, and so on. You have now solved the puzzle: the last number on the billboard is the probability of rain.
In this little puzzle, the first three quantities reported on the billboard are ontic, and you were able to figure out what they corresponded to by measuring aspects of the weather (i.e. elements of reality). The probability of rain was much harder for you to figure out, because it is an epistemic quantity—something of a completely different nature. It is the weather forecaster’s belief (perhaps an unrealistically accurate one) about the weather. There is nothing in the real world that is 40% when the probability of rain is reported as 40%.
With this distinction between ontic and epistemic things, we are now ready to ask: is the quantum state ontic or epistemic? We will call a theory in which quantum states are states of reality $\psi$-ontic, and one in which quantum states are states of knowledge $\psi$-epistemic.
Among the existing interpretations of quantum theory, it sure looks like the $\psi$-ontic view is dominant. In fact, a number of interpretations take the $\psi$-complete position, which is that the quantum state alone is a complete description of reality. Interpretations taking this position include the many worlds interpretation, which is the subject of my last blog post. Perhaps more prominently, this is also the position endorsed by the “orthodox” interpretation that is presented in many textbooks on quantum mechanics. Some textbooks straight up teach it as an axiom of quantum mechanics, such as John Preskill’s lecture notes on quantum information:
Axiom 1. States. A state is a complete description of a physical system. In quantum mechanics, a state is a ray in a Hilbert space.
$\psi$-onticity is a weaker notion than $\psi$-completeness. Hidden variable theories, which posit additional variables that make up the description of reality, often give the quantum state an ontic status. One prominent example of this type of theories is Bohmian mechanics. In Bohmian mechanics, the ontology is posited to be the quantum state, together with some additional variables that are the positions of the particles. Most other ontological models for quantum theory that have been studied to date also regard the quantum state as ontic.
Given this, it might appear that the ontic status of the quantum state is the overwhelming consensus, and the answer to our question is clear. But is there really any evidence that the quantum state is ontic? Could $\psi$-onticity be just like the plausible but ultimately incorrect assumption that the Egyptian hieroglyphs are ideographic? Below, I argue that $\psi$-onticity might be a problematic premise that has been widely internalized without good reasons. I will make this case from two angles: first, why $\psi$-onticity is problematic from the standpoint of locality, and second, why there appears to be strong evidence for the epistemic nature of the quantum state.
Locality
By locality here, I mean the idea that a system can only be influenced by events in its past lightcone. 5 The tension between $\psi$-onticity and locality is not at all subtle, and arguments pointing out this conflict have a long history. Einstein was perhaps the first and most prominent figure to make this point. It is well-known that Einstein was troubled by the $\psi$-complete position, and that he had attempted to construct a hidden variable model of his own. This article analyzes various arguments by Einstein, and argues that he not only argued against $\psi$-completeness, but in fact favored a $\psi$-epistemic interpretation.
Without getting into the historical details, I will present here the simplest way to see the tension between $\psi$-onticity and locality—through the phenomenon of steering. Suppose that Alice and Bob shared a pair of qubits (say, the spin of some particle) in the quantum state $$\ket{\phi^+} = \frac{\ket{+z}\ket{+z} + \ket{-z}\ket{-z}}{\sqrt{2}}.$$ This is a maximally entangled state, and it has the property that if Alice and Bob both measure their spins in the $z$ direction, they are guaranteed to find them in the same direction (either both $+z$ or $-z$). In a bit more detail, it works like this: If Alice measures her qubit in the {$\ket{+z}, \ket{-z}$} basis, quantum theory predicts that she would get outcome $+z$ and $-z$ with 50-50 probability. If she gets outcome $+z$, then the quantum state of her qubit is immediately updated (or collapsed) to $\ket{+z}$, and the quantum state of Bob’s qubit is immediately updated to $\ket{+z}$. This means that Bob is guaranteed to get outcome $+z$ if and when he measures his qubit in the ${ \ket{+z}, \ket{-z} }$ basis as well.
So far so good. Now suppose that Alice instead chooses to measure her qubit in another basis, the {$\ket{+x}, \ket{-x}$} basis, where $\ket{\pm x} = (\ket{+z} \pm \ket{-z})/\sqrt{2}$. In physical space, $+x$ is a direction perpendicular to the $z$-axis, and $-x$ is the opposite direction from $+x$. Since the entangled state they share can be equivalently rewritten as $$\ket{\phi^+} = \frac{\ket{+x}\ket{+x} + \ket{-x}\ket{-x}}{\sqrt{2}},$$ Alice would still get outcome $+x$ and $-x$ with 50-50 odds. And if she got outcome $+x$, that would update the quantum state of her qubit to $\ket{+x}$, and that of Bob’s qubit to $\ket{+x}$, guaranteeing that he gets the $+x$ outcome when measuring his qubit in the same basis. This way, Alice and Bob would still find their spins in the same direction.
To bring locality into the picture, now note that the above analysis holds no matter how far apart Alice and Bob are separated. Quantum theory predicts that Alice’s measurement on her qubit instantaneously changes the state of Bob’s qubit, even when they are on opposite sides of the galaxy. In particular, by choosing to measure her qubit in the {$\ket{+z}, \ket{-z}$} basis, Alice can make Bob’s qubit to be in either state $\ket{+z}$ or state $\ket{-z}$, whereas by measuring her qubit in the {$\ket{+x}, \ket{-x}$} basis, she makes Bob’s qubit be in one of $\ket{+x}$ and $\ket{-x}$ instead. This is very problematic if one believes that $\ket{+z}, \ket{-z}, \ket{+x}, \ket{-x}$ are all distinct states of reality—this means that Alice’s action can instantaneously influence the reality lightyears away. This phenomenon is precisely what Einstein termed “spooky action at a distance” 6.
If one takes the perspective that quantum states are states of knowledge, i.e. are epistemic, however, then they would not find the steering phenomenon troubling at all. The instantaneous update on the quantum state of Bob’s qubit is simply a Bayesian update that Alice performs on her state of knowledge about Bob’s qubit, and no superluminal physical influences are needed. That the quantum state must be a state of knowledge is in fact the most natural lesson to draw from the steering phenomenon.
Unfortunately, the story is not so simple. Since Bell published his seminal 1964 paper, we now know that locality nevertheless fails even if quantum states are regarded as epistemic. The failure comes from the fact that a $\psi$-epistemic explanation still needs to account for the correlation of Alice’s and Bob’s measurement results (always anticorrelated, in the case of the singlet). Bell’s theorem tells us that even if quantum states are regarded as epistemic, there can be no locally causal account of what quantum theory predicts. (If you are intrigued by this, stay tuned for my next blog post, which will be on Bell’s theorem!) Nonetheless, the problem with locality is so obvious if the quantum state is ontic that we would not have needed the “big guns” of Bell’s theorem.
So what other aspects of quantum theory favor a $\psi$-epistemic interpretation over a $\psi$-ontic one? Turns out, it’s most of quantum theory.
Spekkens’ toy model
What is your favorite quantum phenomenon? Entanglement? Teleportation? How about the weirdest, “quantumest” quantum phenomenon? Non-commutativity of measurements? Interference? The no-cloning theorem?
Let me now present to you a classical model that contains all of the above “quantum” phenomena. This model is astoundingly simple to describe and easy to undestand. One basically just needs two insights to have come up with it oneself: One, identify quantum states as states of knowledge about some underlying, real, ontic states. Two, impose a fundamental restriction on the amount of information that can be known. Do this with a discrete ontic state space, and you get Spekkens’ toy theory 7.
One toy bit
A “toy bit”, the smallest fundamental system in this model, can be found in four possible ontic states. In other words, the ontic state space of a toy bit contains four ontic states. To describe this theory, it turns out that a graphical notation is most convenient. A toy bit is usually represented as a 2x2 box, and these are the four possible ontic states of a toy bit:
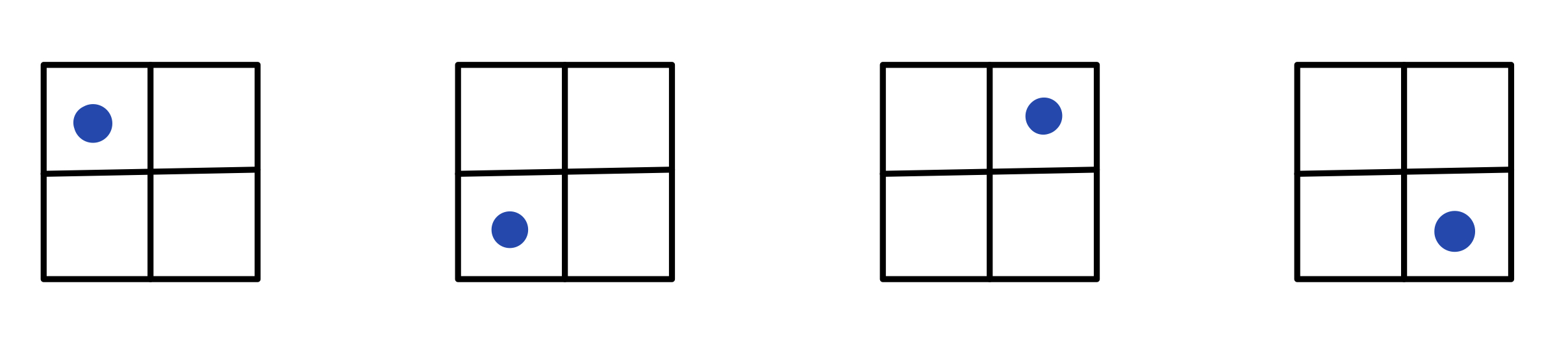
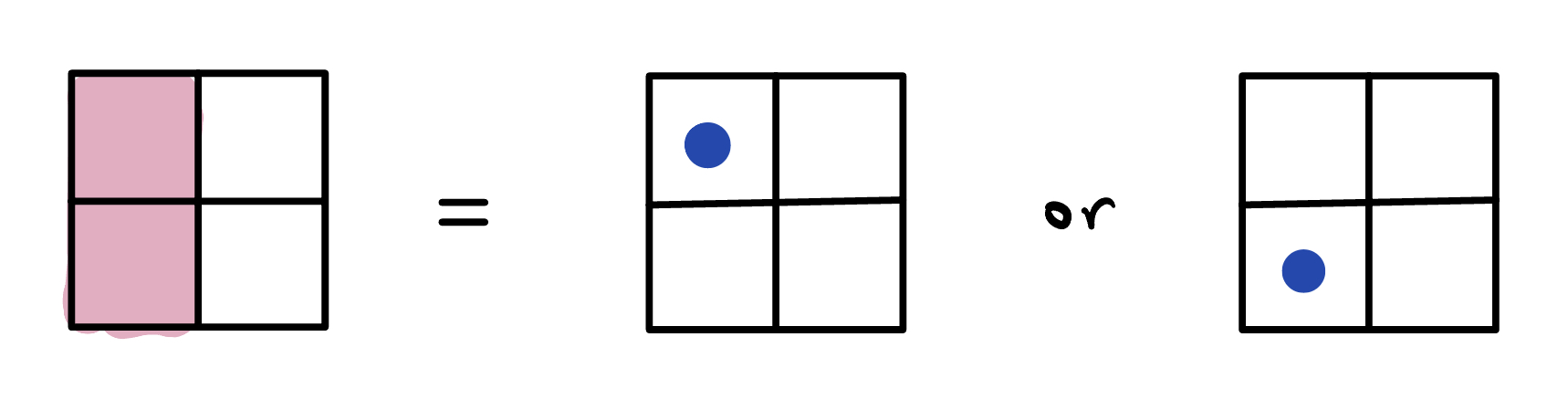
The crucial ingredient of this theory is an epistemic restriction—a fundamental limit on the amount of knowledge that any agent can learn about a system. For a toy bit, it is posited that no agent can ever learn its ontic state exactly. Instead, the best they can do is to narrow it down to one of two possibilities. This gives rise to the notion of an epistemic state, a state of knowledge of some agent. In this graphical notation, an epistemic state is represented as a pattern of shaded boxes. For example, the picture on the left is a possible epistemic state, which in turn means that the ontic state is known to be one of the two possibilities on the right.
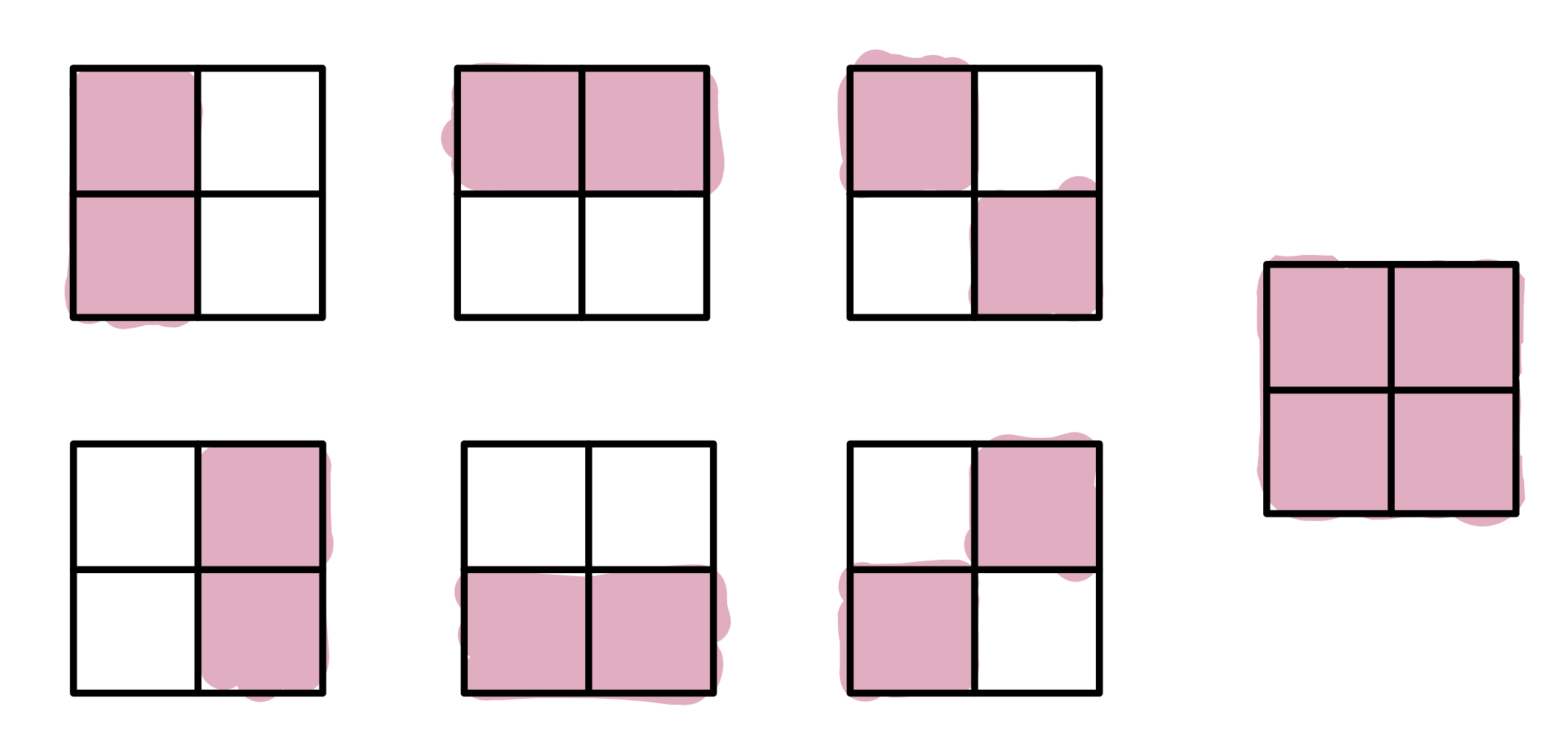
The epistemic restriction means that there are only seven permitted epistemic states for a toy bit, as shown below. It is also possible to know nothing about a toy bit.
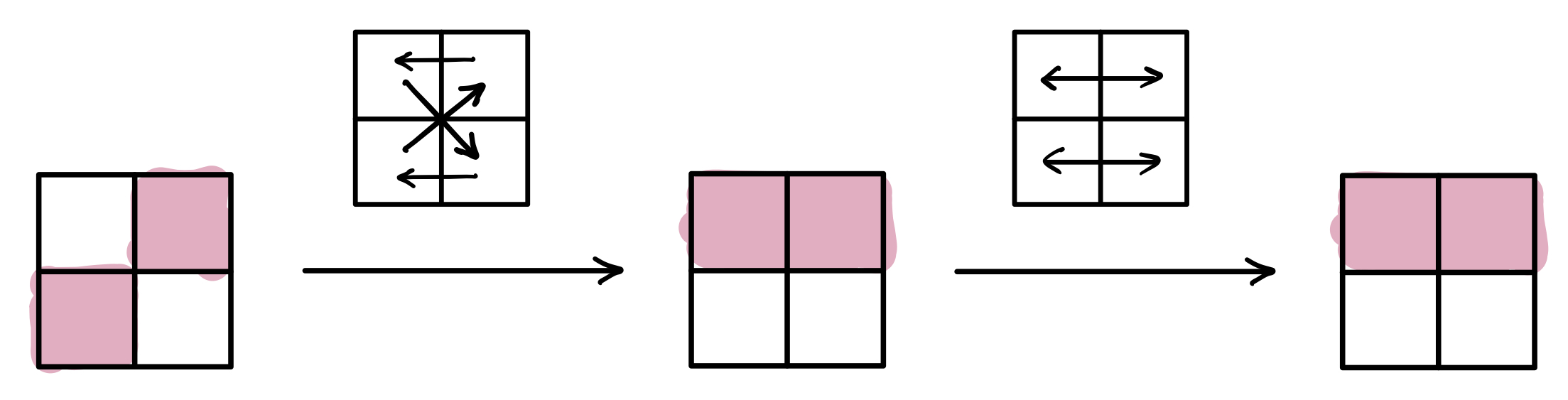
For this to be a complete theory, we need to know how a toy bit evolves, and how it behaves when undergoing measurements. We won’t go into the details, but in order to preserve the epistemic restriction, it turns out that the only permitted transformations are permutations of ontic states. This means that we can only shuffle the four ontic states around. The shuffling in turn determines how the epistemic state is going to change. For example, below is a series of valid transformations, and their effects on an epistemic state. As we see with the second transformation, sometimes nontrivial transformations can leave the epistemic state unchanged.
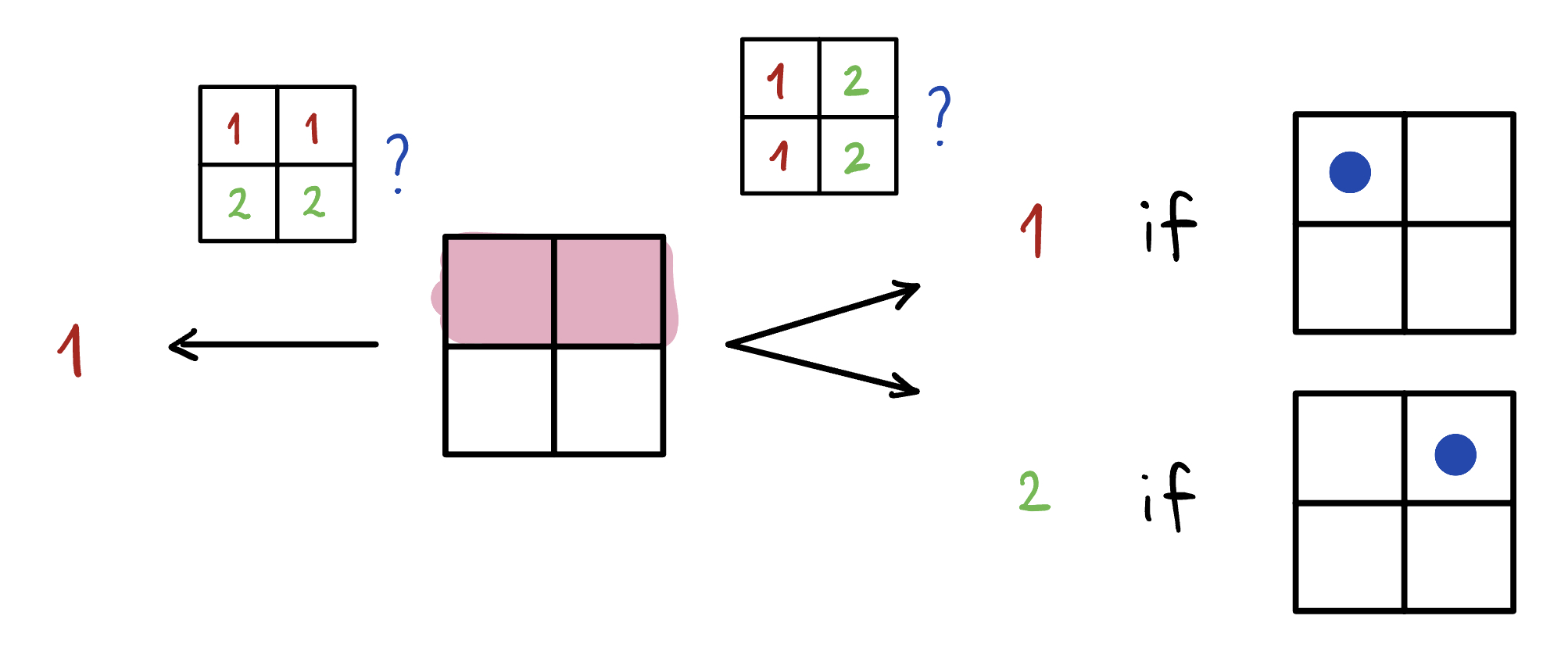
When a measurement is made on a toy bit, it also is not allowed to violate the epistemic restriction. This means that one is never allowed to ask which ontic state the toy bit is in. In fact, all allowed measurements are of the form, “which of the two regions is the ontic state in?” In other words, a measurement can only reveal one bit of information. This means also that the measurement outcome is decided deterministically by the ontic state that the toy bit is in. In the examples below, the measurement on the left gives outcome 1 deterministically, whereas the measurement on the right returns both outcomes with equal probability. To see why that is, recall that the epistemic state that we are given means that the ontic state is either in the top left (TL) or top right (TR). For both possibilities, when faced with the left measurement (“are you in the top or bottom half?”), the answer is 1. But for the right measurement (“are you in the left or right half?”), TL is going to give outcome 1, while TR gives outcome 2. Since it is not possible to know whether the ontic state was TL or TR to start with, what is observed given this initial epistemic state is that the measurement yields outcomes 1 and 2 with equal probability.
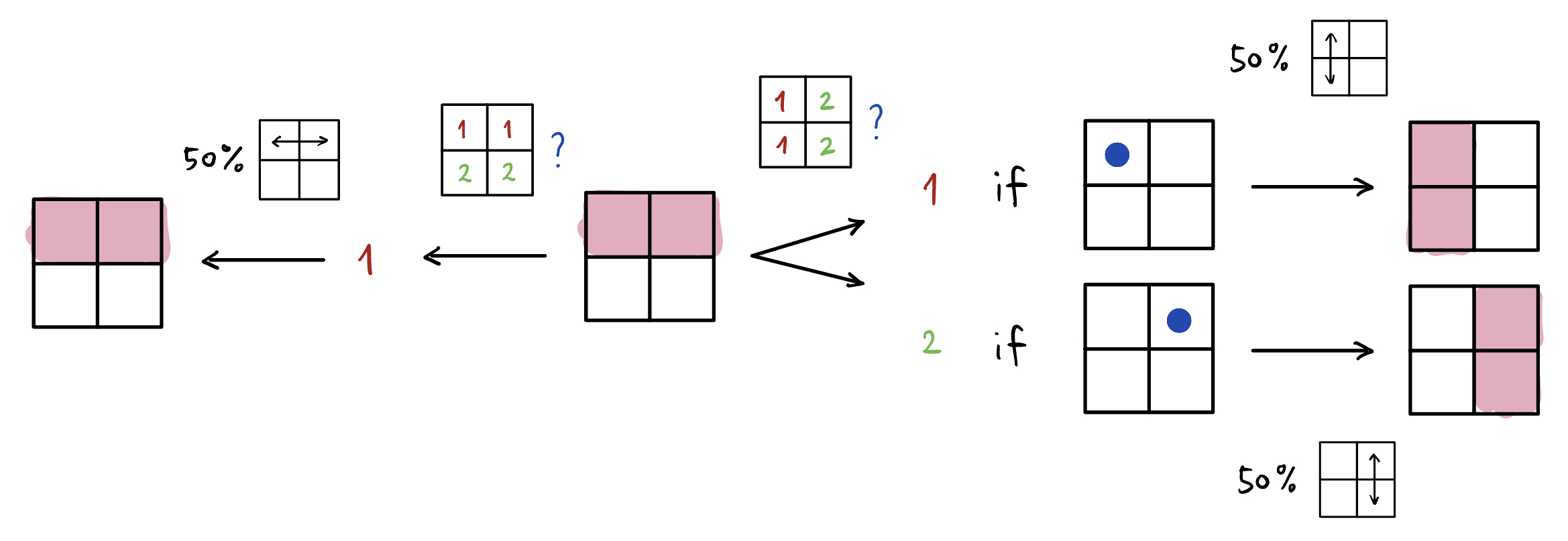
To complete the description of measurements, one final step is needed. For the measurement on the right, note that the measurement result reveals the exact ontic state of the toy bit: TL for outcome 1, and TR for outcome 2. If nothing else happens, then we would have learned more than what is allowed by the epistemic restriction. To preserve the epistemic restriction, then, measurements will necessarily introduce a disturbance, and reshuffle the ontic states within each of the two regions. Formally, this reshuffle is equivalent to doing nothing with 50% probability, and permuting the two ontic states in the region corresponding to the measurement outcome with 50% probability. The end effect of the disturbance is to reprepare the toy bit to be in an epistemic state so that if the measurement were repeated, it is guaranteed to yield the same outcome. In the example above, for the measurement on the right, this updates the epistemic state of the toy bit post-measurement, whereas the epistemic state is left unchanged for the measurement on the left.
Hopefully, you can already see the shadows of some familiar quantum phenomenology. Remember that quantum states are analogous to the epistemic states in this theory. For example, it is clear that wavefunction collapse, which is a truly pretty problematic process if one thinks the wavefunction is ontic, is nothing more than the epistemic update upon learning new information after a measurement (and accounting for the disturbance it introduces). As another example, it is also easy to see that the two measurements discussed in the example above don’t commute: doing the left measurement first deterministically yields outcome 1, whereas if it is done after the right measurement, both outcomes are 50-50. This looks an awful lot like the basic behavior in Stern-Gerlach experiments: measuring the spin along the $z$-axis does not commute with measuring it along the $x$-axis.
Indeed, if you are familiar with the quantum theory of qubit, this identification is almost exact:
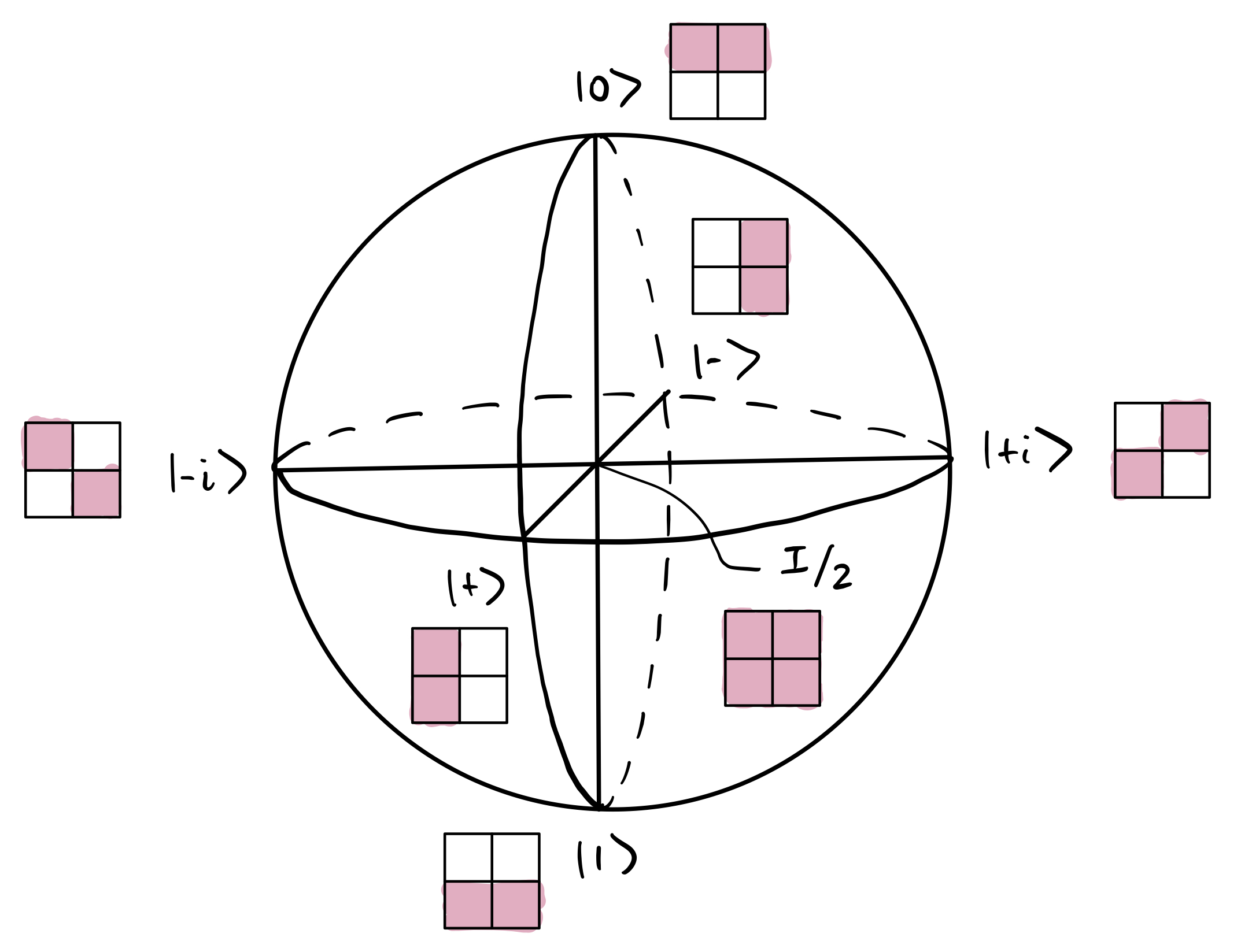
(In case you are not familiar with this picture, I’m drawing a Bloch sphere, which is a common way to visualize the state space of a qubit.)
However, many interesting quantum phenomena only occur when more than one system is considered, such as entanglement, steering, and teleportation. Let us now focus our attention on how the toy theory describes two toy bits—the smallest composite system. We will see that the phenomenology here also closely mirrors that of quantum theory.
Two toy bits
Since each toy bit has four ontic states, a pair of toy bits has sixteen ontic states: one just needs to specify the ontic state of toy bit 1, and then the ontic state of toy bit 2. We usually represent a pair of toy bits by a 4x4 box. For example, for a toy bit whose ontic state is known to be in the left half, and another whose ontic state is known to be in the right half, the epistemic state of the combined system is this:
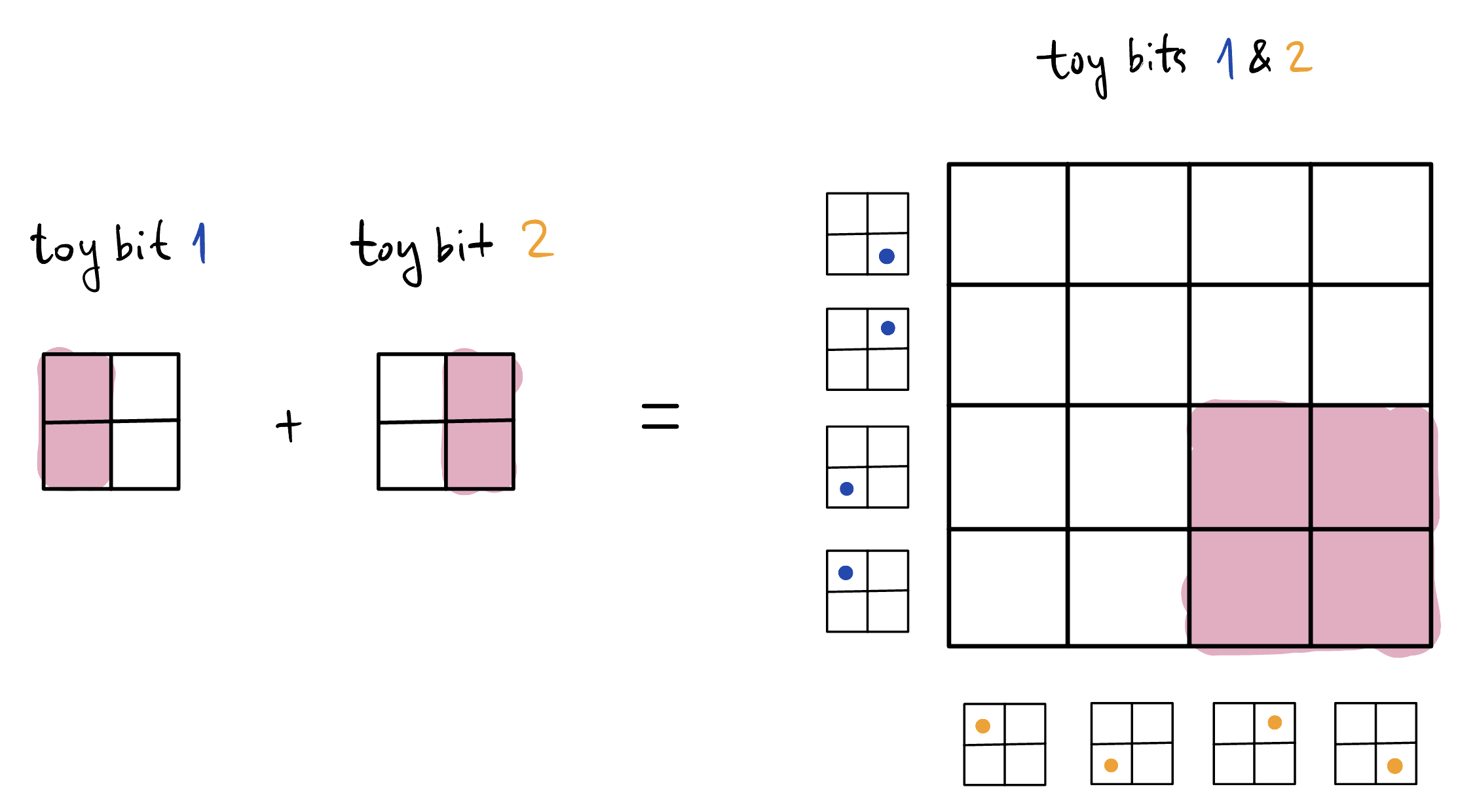
It turns out that this epistemic state achieves the maximal amount of knowledge allowed on a pair of toy bits—narrowing the ontic state down to four possibilities. In this case, it corresponds to knowing one bit of information about each toy bit. Interestingly, there is a different class of epistemic states that also attain maximal knowledge, such as this one below.
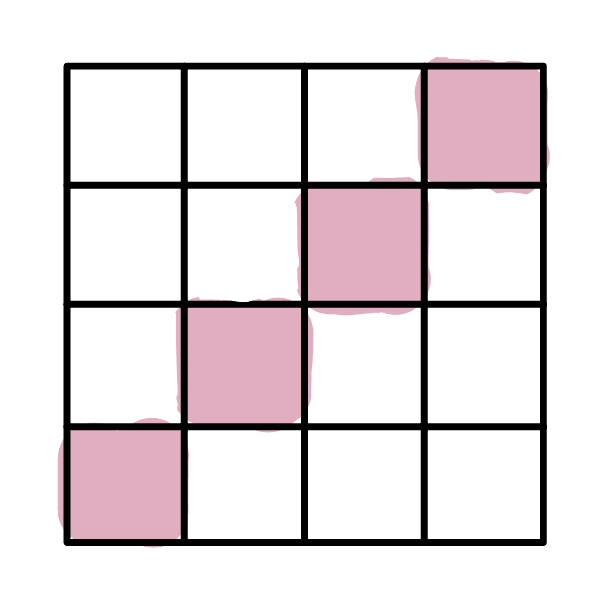
For this epistemic state, we are completely uncertain about the ontic state of either toy bit—the marginal distribution on each toy bit spans all four ontic state. However, we know that the ontic states of the two bits are perfectly correlated: either they are both in the top left, or both in the top right, and so on. This is analogous to an entangled state, whereas the epistemic state in the first example is analogous to a product state.
Indeed, we can now reproduce the phenomenon of steering with this “entangled” epistemic state. In the steering discussion above, Alice and Bob share the maximally entangled state $\ket{\phi^+}$, and Alice can choose to measure her qubit in either the {$\ket{+z}, \ket{-z}$} basis, or the {$\ket{+x}, \ket{-x}$} basis. Here, Alice and Bob would share two toy bits in this “entangled” epistemic state, and Alice can choose to perform the measurement “left or right?” or measurement “up or down?”. Since this epistemic state is one of complete ignorance about the ontic state of Alice’s toy bit, both outcomes are possible no matter which measurement Alice chooses. However, since the epistemic state is also one that encodes perfect correlation between Alice’s and Bob’s toy bits—whatever ontic state Alice’s is in, so is Bob’s—Bob is guaranteed to get the same outcome when he performs the same measurement. Furthermore, Alice’s measurement on her toy bit introduces a disturbance on her toy bit in order to preserve the epistemic restriction, in the manner described above. This in turn induces a disturbance on the joint epistemic state, and allows Bob’s toy bit to be “steered” into different epistemic states. However, it is clear that no changes whatsoever have happened to the ontic state of Bob’s toy bit, as all the transformations only permute ontic states in the vertical direction. Within the toy theory, steering can be clearly understood as a combination of local ontic actions plus an epistemic update, and certainly at no point requires any spooky action at a distance.
Finally, we are now ready to discuss how a version of the quantum teleportation protocol works in the toy theory. For those that are not familiar, quantum teleportation is a procedure that allows one party to send a quantum state to another, given that they have shared some quantum resource (i.e. entanglement) beforehand and have a means of communicating classically. The surprising thing about this protocol is that an arbitrary quantum state on a qubit can be teleported this way with only 2 bits of classical communication. Quantum states on a qubit are of the form $a \ket{0} + b\ket{1}$, where $a$ and $b$ are complex numbers, and theoretically requires an infinite amount of information to specify completely. The possibility of quantum teleportation is regarded by many as a proof that the information processing capacity of quantum theory fundamentally exceeds that of classical theories, and as a culmination of quantum weirdness.
Here is how the procedure works. Alice has an arbitrary quantum state $\ket{\psi}$ that she wishes Bob to have. Note that she does not need to know what $\ket{\psi}$ is. To run the teleportation protocol, Alice and Bob have previously prepared an entangled pair of particles to be in the state $\ket{\phi^+} = (\ket{00} + \ket{11})/\sqrt{2}$ and each taken one with them. To teleport her qubit, Alice needs to do two things: First, she performs a joint measurement on the qubit she wishes to send and her half of the entangled pair, in the so called Bell basis, {$\ket{\phi^+}, \ket{\phi^-}, \ket{\psi^+}, \ket{\psi^-}$}. The basis states are called Bell states, and are all maximally entangled: $$\ket{\phi^\pm} = \frac{\ket{00} \pm \ket{11}}{\sqrt{2}},$$ $$\ket{\psi^\pm} = \frac{\ket{01} \pm \ket{10}}{\sqrt{2}}.$$
She is bound to get one of the four outcomes from this measurement, and no matter what outcome she gets, she picks up the phone and text Bob her measurement outcome. With this information, Bob applies a unitary transformation to his half of the entangled pair, according to this table:
| Alice’s outcome | Bob’s action |
|---|---|
| $\phi^+$ | do nothing |
| $\phi^-$ | apply $\sigma_z$ |
| $\psi^+$ | apply $\sigma_x$ |
| $\psi^-$ | apply $\sigma_z\sigma_x$ |
Since there are only four possible outcomes, only two bits of information need to be communicated. With a few lines of calculation, one can verify that the quantum state of Bob’s particle is now $\ket{\psi}$, the original state that Alice wished to teleport. The protocol can be summarized diagrammatically as below.
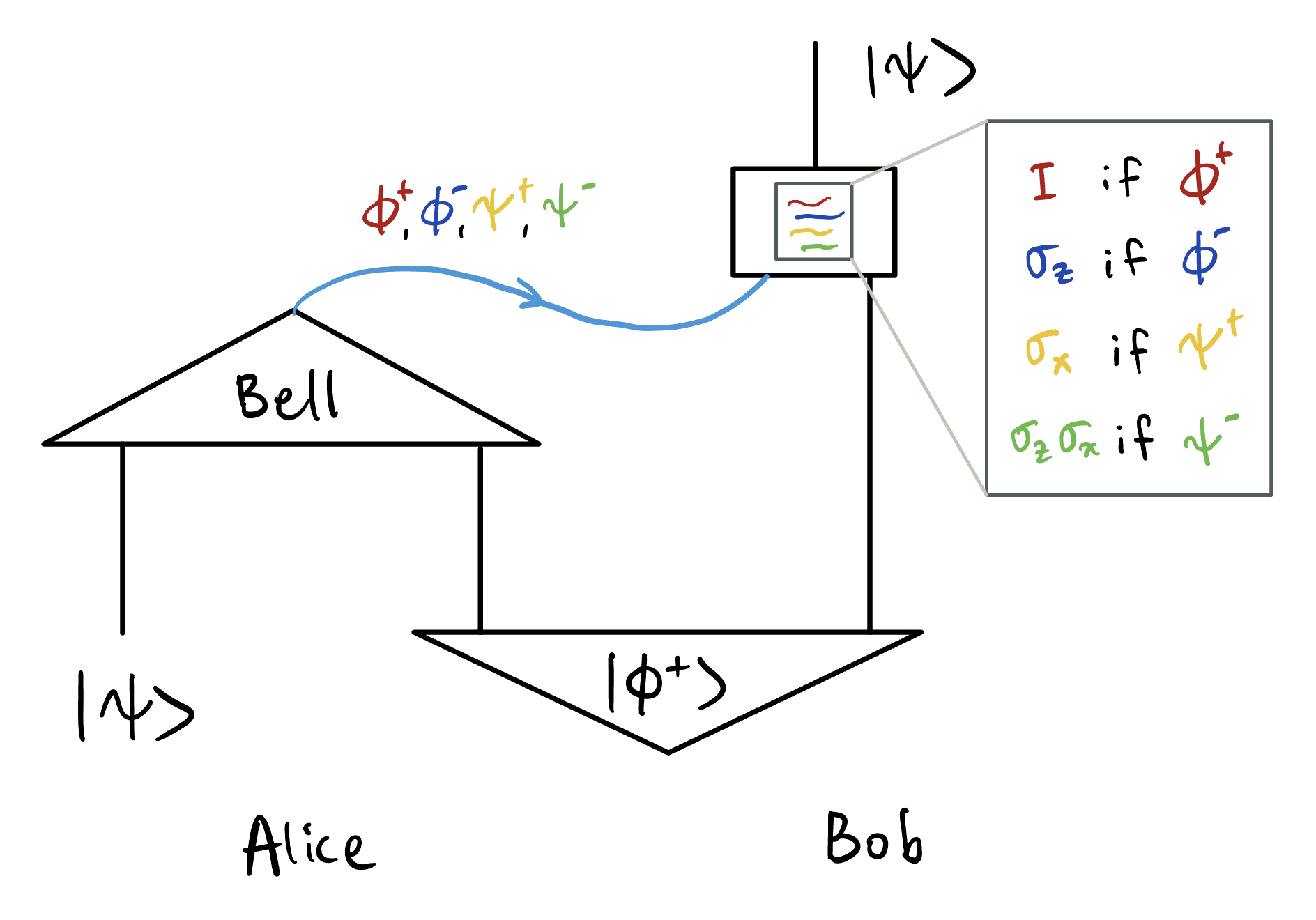
At face value, this is pretty strange. There seems to be no analogue of this in the classical world. But it is certainly not as strange as some make it to be—for instance, it is clear that despite the name “teleportation”, this protocol is not instantaneous and does not allow for faster-than-light communication, since Alice must let Bob know her measurement outcome via some form of classical communication. It is commonly agreed upon that the core mystery here is one of compression: how come Alice can send Bob an arbitrary, unknown state, effectively communicating an infinite amount of information, by only actually sending him two bits?
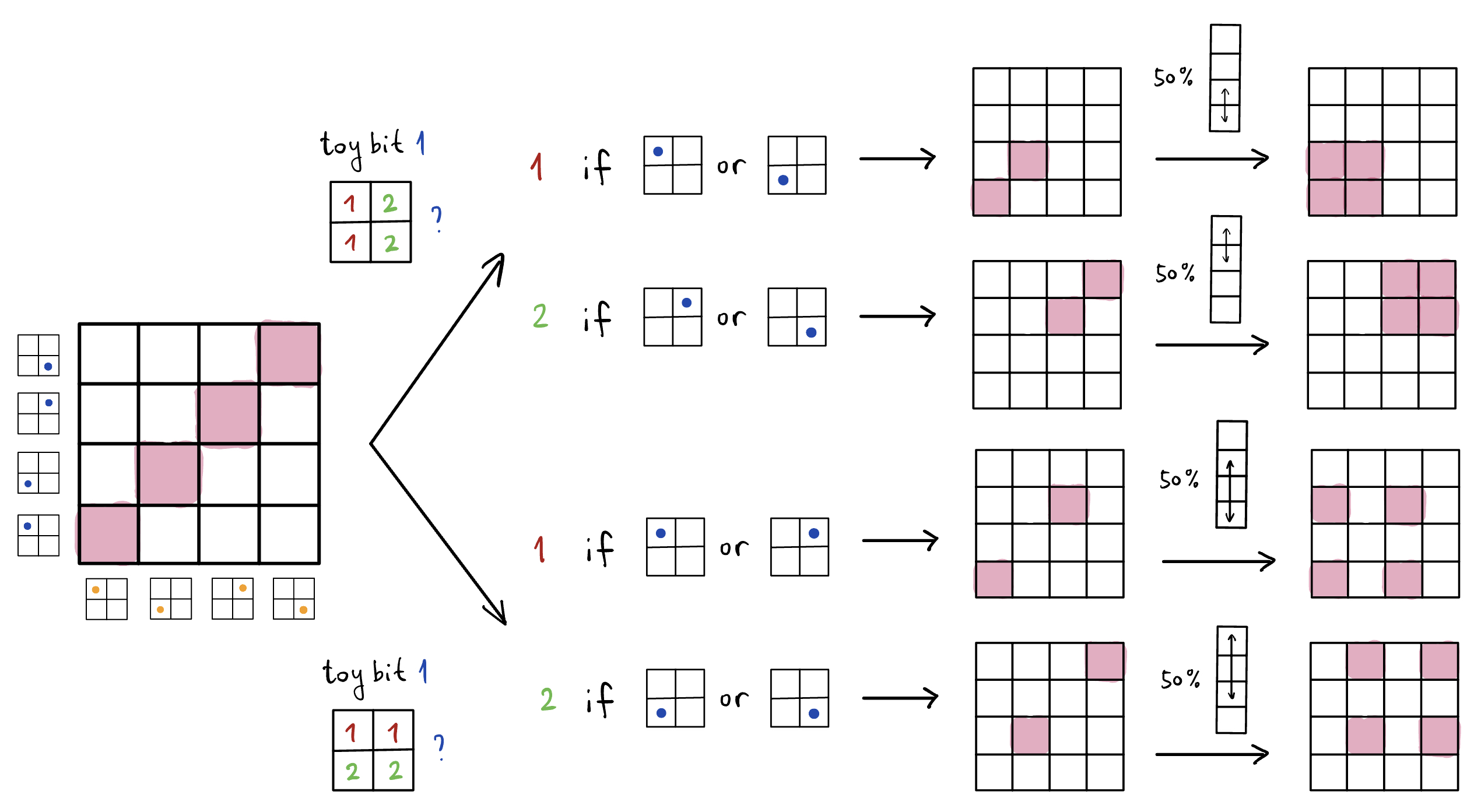
The answer that Spekkens’ toy theory would give is, unsurprisingly, that this is because the quantum state that Alice manages to teleport is a state of knowledge, not a state of reality. Indeed, one can almost completely reproduce the teleportation protocol in the toy theory. Alice and Bob would need to pre-share an “entangled” pair of toy bit, in the joint epistemic state of perfect correlation discussed above. Similar to a measurement in the Bell basis, Alice now performs this measurement on the toy bit she wishes to teleport and her half of the “entangled” pair:
It is clear that conceptually, this is the measurement that reveals the relationship between two toy bits—outcome 1 means that the two toy bits are in the same ontic state, and outcome 4 means that the two toy bits are in “opposite” ontic state, where the opposite of top left is bottom right, and so on. (If this is not clear to you, refer back to the labels of what each row and column corresponds to in the 4x4 box a few figures back.)
So Alice learns the precise relationship between her two toy bits, and then texts Bob the outcome of her measurement (1, 2, 3, or 4), and upon receiving Alice’s text, Bob now performs one of four permutations on the ontic states of his toy bit as pictured below.
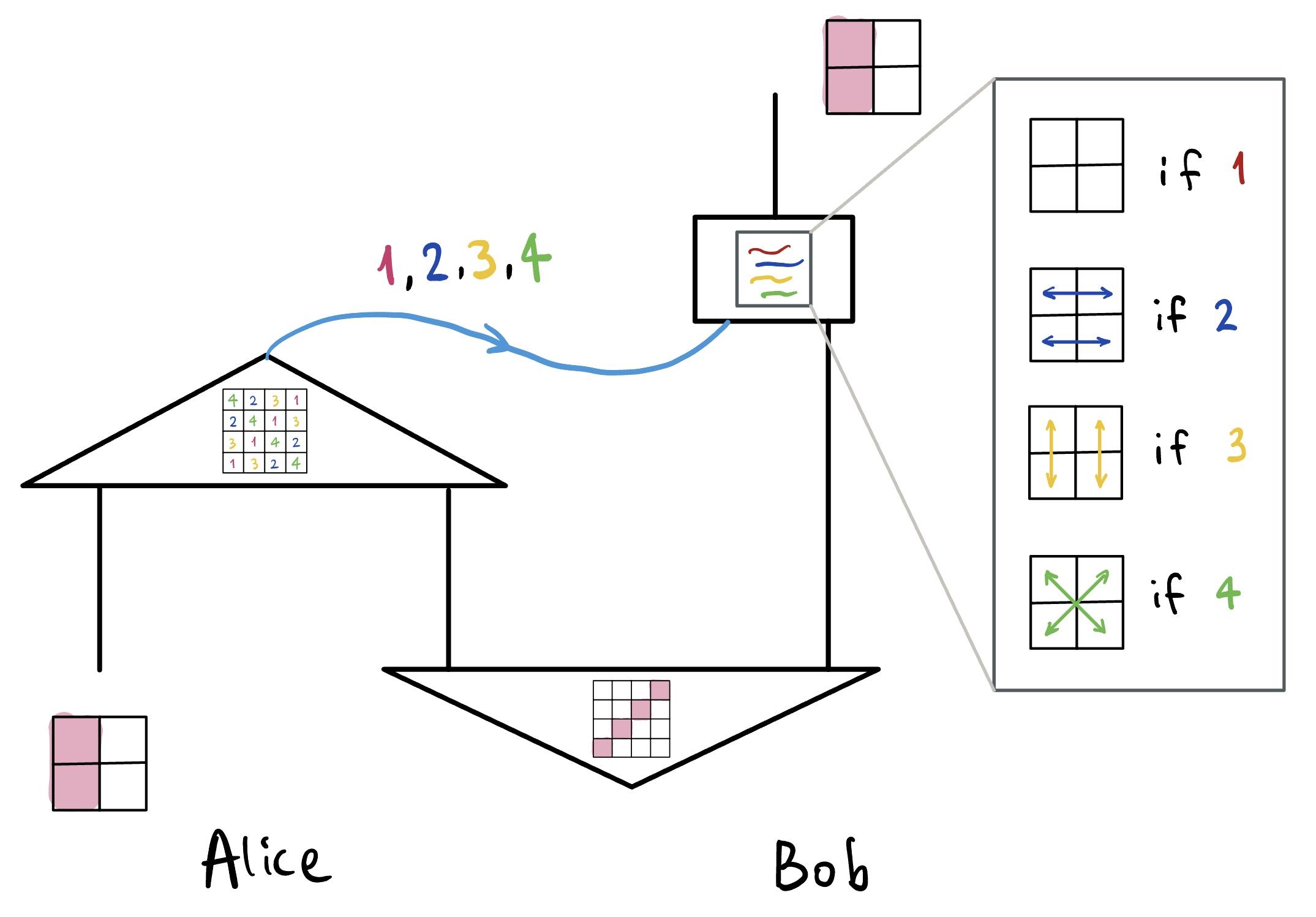
Conceptually, it is not too hard to explain why this would work. Alice and Bob start off by sharing a pair of toy bits, and while they do not know anything about their individual ontic state, they know that they are in the same ontic state. Then, Alice performs a measurement to figure out the relationship between the ontic state of the toy bit that she is teleporting, and that of her half of the entangled toy bit pair. Say that she gets outcome 1. That would mean that she now knows that the toy bit to be teleported is in the same ontic state as her half of the entangled pair, and hence also the same ontic state as Bob’s half. Now, since quantum states are states of knowledge, teleporation is a task where the goal is to make one’s knowledge about one system be applicable to another system. If Alice tells Bob that she got outcome 1, then Bob would know that he doesn’t need to do anything, and the state of knowledge on Alice’s original toy bit is already applicable to Bob’s toy bit. Similarly, if Alice gets outcome 2, then Bob knows that in order to get his toy bit to be in the same ontic state as Alice’s original toy bit, he needs to perform the permutation that swaps his toy bit left and right. After the permutation, Alice’s (or someone else’s, since Alice does not necessarily know the state of the toy bit that she is teleporting) original description would now work for Bob’s toy bit.
At the same time, this protocol retains the flavor of surprise in teleportation, because there are six allowed epistemic states on a toy bit (excluding the one of complete ignorance), and still only two bits need to be communicated for Alice to teleport her toy bit. $\log_26$ is still greater than 2, albeit not infinite. Nonetheless, since the nature of teleportation is not actually transporting anything in reality, and is just about transferring the applicability of some knowledge, it is not that surprising that it requires less communication than is naively expected.
What the toy model tells us
I have said plenty about the specifics of Spekkens’ toy theory, and hopefully gave a flavor of how it explains various quantum phenomenoma by resorting to the postulate that quantum states are states of knowledge. While this theory is opertionally distinct from quantum theory—roughly speaking, while quantum theory corresponds to the whole Bloch ball (i.e. surface + interior), the toy theory only corresponds to the octahedron formed by connecting the six labeled points on the Bloch sphere, called the stabilizer subtheory of quantum theory8—it comes extremely close to quantum theory in the sense that it contains a long list of phenomena that feature in quantum theory that are normally considered nonclassical, while failing to reproduce only a few quantum phenomena. It essentially sorts quantum phenomenology into two buckets, by the following table:
| appears in toy theory | does not appear in toy theory |
|---|---|
| noncommutativity of measurements | Bell inequality violations |
| collapse | noncontextuality inequality violations |
| coherent superposition | computational speedup (if exists) |
| no-cloning | |
| interference | |
| ambiguity of mixtures | |
| entanglement | |
| steering | |
| teleportation | |
| and some more … |
There are many reasons why I find the toy theory so exciting. For one, it clarifies that there are at least two varieties of nonclassical phenomena: those that arise in a classical theory with an epistemic restriction, and those that cannot be reproduced in such a theory. This provides us with a simple method to assess the nonclassicality of any seemingly strange phenomenology: is it reproducible in the toy theory, or not? In other words, we now have a principled way to answer the question, “What is so weird about quantum mechanics?” Instead of resorting to personal wisdom such as the well-known Feynman quote that interference phenomena “contain the only mystery [of quantum mechanics]” 9, we now know that nonlocality and contextuality are the true mysteries of quantum mechanics. To crack open the strange case of quantum theory, we must focus our effort on understanding those.
To me, Spekkens’ toy model is also the single most suggestive piece of evidence about the nature of the quantum state. In the table above, one can’t help but notice that the list on the left is very long, and the list on the right is very short. All but a handful of the phenomena we consider quantum are captured by Spekkens’ toy model, which is just a classical theory of (restricted) information. It is natural to ask, why? Why is the toy theory so good at producing quantum phenomena and explaining them in terms of a theory of information? And the most logical answer for this is clear: it must be the case that quantum theory is a theory of information. To me, the explanatory power provided by the toy theory is an unequivocal piece of evidence showing that the quantum state is a state of knowledge, rather than a state of reality.
Concluding thoughts
To conclude, I would like to revisit the analogy with the decipherment of Egyptian hieroglyphs. I want to make the parallel completely explicit. In the case of hieroglyph decipherment, the incorrect assumption that the hieroglyphs are ideographic hindered progress for a millennium. The assumption was plausible, but was fundamentally not grounded in empirical evidence, and simply passed down by generations of scholars without anyone thinking to question it. Even after it was found that the hieroglyphs were phonetic when appearing in cartouches, Champollion was slow to generalize this insight to the rest of the script, because he was held back by the false premise.
Could this be what’s going on with the interpretation of quantum mechanics, too? The dominant view passed along by our textbooks and existing interpretations is that the quantum state is ontic, a state of reality. This is certainly plausible, but not only is there no good evidence supporting it, it leads to problematic conflict with locality quite readily (at least more readily than with the $\psi$-epistemic view). Spekkens’ toy model shows that at least in the context of a subtheory of quantum theory, quantum states behave as if they are states of knowledge. If the parallel with the hieroglyph story continues to hold, then, maybe what will lead to an eventual breakthrough in the interpretation of quantum theory is to embrace the fact that the quantum state is a state of knowledge in general.
All this to say, it is not that I think the $\psi$-epistemic position must be 100% correct. The bottom line is, it is simply makes no sense that essentially all interpretational effort has been put into the $\psi$-ontic basket, whereas there is very good evidence that the $\psi$-epistemic approach is also worth investigating, if not more so. Given the evidence on the table, especially Spekkens’ toy model, I also think that now any satisfactory interpretation of quantum theory, especially ones that take the $\psi$-ontic approach, must pass the bar of explaining why the quantum state behaves so much like a state of knowledge.
Finally, let me end by saying that we are probably pretty far from the end of the story, even if you are sympathetic to the $\psi$-epistemic view. We are not where Champollion was in July 1822. If quantum states are states of knowledge, the problem is that we have no idea what the knowledge is about. Restricted knowledge about four ontic states gave us something very close to the quantum theory of a qubit, but we know that we can’t get much closer with simple modifications to Spekkens’ toy model, because of two classes of no-go theorems—Bell-like theorems and contextuality no-go theorems. At the end of the day, Spekkens’ toy model is a local, noncontextual ontological model, and we know that we must go beyond the assumptions of such a model in order to have any hopes of understanding all the mysteries of quantum theory.
Much of this post is based on Rob Spekkens’ excellent public lecture at the Perimeter Institute, The riddle of the quantum sphinx. Rob is an excellent speaker—if you are someone that enjoys lectures, feel free to check it out!
-
It turns out that even the little rectangular box is relevant. It is a vertical stroke that denotes a “determinative”, which serves to distinguish it from other words that are pronounced “sꜣ”. ↩︎
-
This is somewhat of a lucky coincidence, actually. By the 19th century, Coptic was no longer in use other than as the liturgical language of the Coptic Church. Champollion had studied Coptic because of his fascination with ancient Egypt and the connection of Coptic to various ancient Egyptian languages. ↩︎
-
This was, of course, a dramaticized version of the story of how the hieroglyphs were deciphered. The whole script was definitely not deciphered by Champollion alone in one day, and involved a lot more effort by many people for many more years. For a more detailed account of the decipherment of the Egyptian hieroglyphs, see this Wikipedia page. ↩︎
-
“Average cloud cover” is a field reported by the weather app that I use. I didn’t know it is a thing either! ↩︎
-
More precisely, what I described here is the concept of local causality. Locality sometimes encompasses both local causality and a different concept called separability, which is the idea that the complete description of an overall system is simply the combination of descriptions of its constituents. Note that the $\psi$-complete view already violates separability, since by the axioms of quantum theory, we know that quantum states are combined via tensor products, not Cartesian products. ↩︎
-
Note that the usual analysis in a quantum mechanics textbook points out that despite the instantaneous update, Alice and Bob cannot use this to send each other information instantaneously. This is true, but is besides the point. The failure to communicate does not absolve $\psi$-onticity of implying superluminal influences. ↩︎
-
This can be done for continuous ontic state spaces as well! Imposing the same epistemic restriction on a continuous phase space just yields a subtheory of continuous quantum mechanics, called Gaussian quantum mechanics. ↩︎
-
This is technically a little bit wrong. It turns out that the theory of a toy bit is subtly different from the stabilizer subtheory of a qubit, but Catani and Browne has shown that the correspondence is exact for systems of all odd dimensions. This has to do with the fact that the qubit stabilizer subtheory is actually contextual. The toy theory is a noncontextual ontological model, so it cannot possibly reproduce all of the qubit stabilizer subtheory. Contextuality is also on the list of the topics I have planned for the next few blog posts, so stay tuned if you are interested in this point! ↩︎
-
Actually, one can understand all of the standard phenomenology on an interferometer, including the Elitzur-Vaidman bomb tester, using a framework akin to the toy model presented here. If you are interested in how that works, check out this recent paper. ↩︎